Sonora.ID - Materi Matematika kali ini kita akan membahas mengenai bilangan eksponen dan sifat-sifatnya.

Sebenarnya apa sih yang dimaksud dengan bilangan eksponen itu?

Melansir dari buku Buku Pintar Matematika SD, bilangan eksponen merupakan bilangan kecil yang terletak di sebelah kanan atas dari suatu bilangan.

Angka yang menunjukkan banyaknya sebuah bilangan (bilangan pokok) akan dikalikan dengan bilangan itu sendiri.

Bilangan eksponen ini juga lebih dikenal dengan istilah bilangan berpangkat. Pada bilangan berpangkat a³, maka 3 di sinilah yang dinamakan eksponen.

a³ = a x a x a.

Baca Juga: Fungsi Sentrosom pada Sel Hewan Lengkap dengan Penjelasan Strukturnya

Sifat Bilangan Eksponen

Bilangan eksponen ini juga memiliki beberapa sifat yang dapat membantu kita dalam menghitung persamaan dan pertidaksamaannya.

Sifat-sifat bilangan eksponen tersebut di antaranya sebagai berikut.

1. Pangkat Penjumlahan

Jika ada perkalian eksponen dengan bilangan pokok yang sama, maka pangkatnya harus ditambah.

a^m x aⁿ = a^{m + n}

Contoh: 2⁴ x 2² = 2^{4 + 2} = 2⁶ = 64.

2. Pangkat Pengurangan

Jika ada pembagian eksponen dengan bilangan pokok yang sama, maka pangkatnya harus dikurang. 

a^m : aⁿ = a^{m – n}

Contoh: 2⁵ : 2³ = 2^{5 – 3} = 2² = 4.

3. Pangkat Perkalian

Jika ada bilangan berpangkat yang dipangkatkan lagi, maka pangkatnya harus dikali.

(a^m)ⁿ = a^{m x n}

Contoh: (2²)³ = 2^{2 x 3} = 2⁶ = 64.

4. Perkalian Bilangan yang Dipangkatkan

Dalam hal ini maka masing-masing bilangan tersebut harus dipangkatkan juga.

(a . b)^m = a^m . b^m

Contoh: (2 x 3)² = 2² x 3² = 4 x 9 = 36.

Baca Juga: Cara Menghitung Perbandingan, Beserta Berbagai Jenis dan Contohnya

5. Perpangkatan Bilangan Pecahan

Maka bilangan pembilang dan penyebutnya harus dipangkatkan semua, dengan syarat b ≠ 0. Artinya, penyebutnya tidak boleh sama dengan 0.

6. Pangkat Pecahan

Maka dapat dikerjakan dengan rumus berikut.

7. Pangkat Nol

Maka hasilnya sama dengan 1 entah berapapun nilai bilangan pokoknya, dengan syarat bahwa bilangan posoknta tidak sama dengan 0 atau (a ≠ 0).

a⁰ = 1, untuk a ≠ 0

Contoh: 2⁰ = 1.

8. Pangkat Negatif

Maka nilainya sama dengan 1 per bilangan eksponen tersebut, namun pangkatnya menjadi positif.

Baca Juga: 6 Contoh Soal Persamaan Linear Dua Variabel, Lengkap dengan Jawaban

9. Bilangan Negatif Berpangkat Ganjil

Jika dipangkatkan dengan bilangan ganjil, maka hasilnya adalah bilangan negatif.

(-a)^m = -a^m , dengan m = ganjil

Contoh: 

(-2)³ = -(2³)

(-2) x(-2) x(-2) = -(2 x 2 x 2) = -8.

10. Bilangan Negatif Berpangkat Genap

Sebaliknya, jika dipangkatkan dengan bilangan genap, maka hasilnya adalah bilangan positif.

(-a)ⁿ = aⁿ , dengan n = genap

Contoh:

(-2)² = 2²

(-2) x(-2) = 2 x 2 = 4.

Contoh Soal

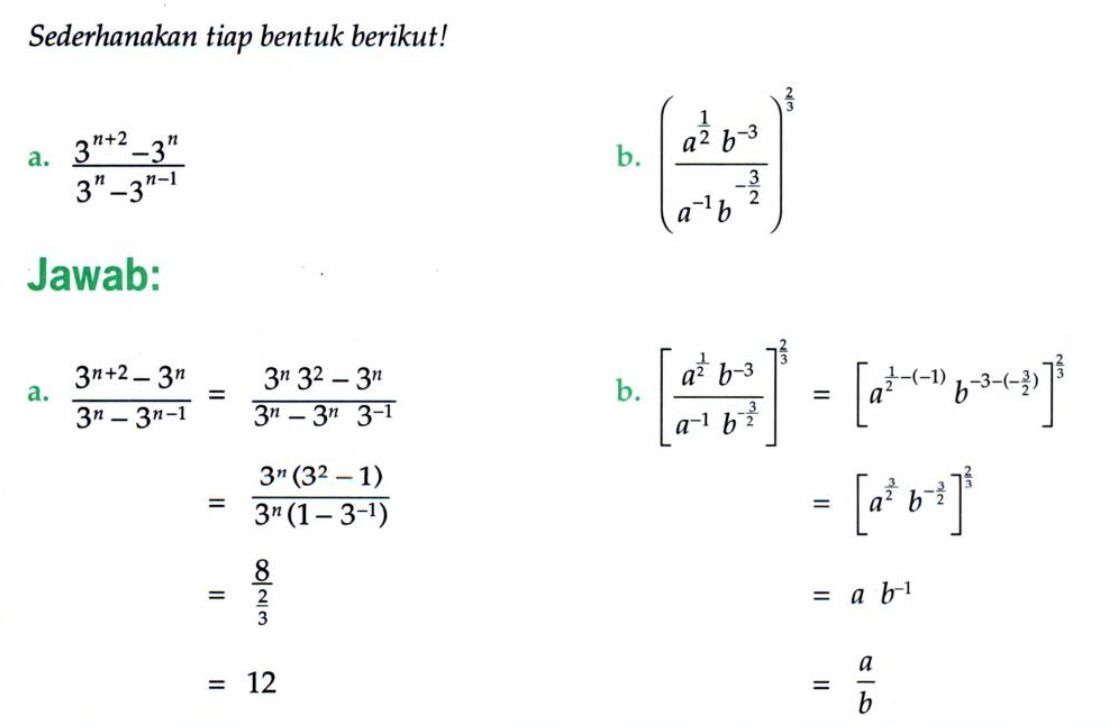
Baca Juga: 5 Contoh Soal Induksi Matematika Kelas 11 Lengkap dengan Kunci Jawaban

Baca berita update lainnya dari Sonora.id di Google News.