Sonora.ID - Materi Matematika SMA kali ini kita akan membahas secara mendalam mengenai permutasi. Apa yang dimaksud dengan permutasi itu?

Mengutip dari buku Super Bank Soal Matematika SMA Kelas 1, 2, & 3, permutasi merupakan cara penyusunan unsur-unsur atau elemen-elemen dengan memerhatikan urutan.

Ada berbagai jenis serta rumus permutasi yang dapat digunakan untuk memecahkan suatu masalah di antaranya adalah sebagai berikut.

1. Permutasi dengan sebagian unsur

2. Permutasi dengan semua unsur

3. Permutasi dengan unsur yang sama

Banyaknya permutasi n unsur dengan x dan y unsur yang sama.

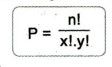
4. Permutasi berulang

Banyaknya permutasi dari n unsur diambil r unsur berulang.

5. Permutasi siklis (melingkar)

Banyaknya permutasi siklis (melingkar) dari n unsur.

Berikut ini pun beberapa contoh soal permutasi lengkap dengan pembahasannya.

Baca Juga: Cara Mencari FPB dan KPK Materi Matematika, Lengkap dengan Contoh Soal

Contoh Soal Permutasi

1. Pada suatu acara makan siang kerajaan yang dihadiri oleh 8 orang, para tamu makan dengan posisi duduk melingkar. Banyaknya susunan yang bisa dibuat saat mereka duduk adalah

Jawaban:

Permutasi

(n-1)! = (8-1)!

7! = 7x6x5x4x3x2x1

= 5040

2. 

3. Seorang fotografer pernikahan harus memanfaatkan waktu dengan baik. Ia hendak mengambil foto dari 10 tamu yang merupakan kerabat dekat. Mereka ingin berfoto secara bergantian dengan susunan 5 orang 5 orang berjejer dari kanan ke kiri. Banyak posisi foto yang dapat dipilih pada saat sesi pertama adalah…

Jawaban:

P(n,r) = n!/(n-r)!

P(10,5) = 10!/(10-5)!

= 10 x 9 x 8 x 7 x 6 x 5! / 5!

= 10 x 9 x 8 x 7 x 6

= 30.240

4. 

5. Seorang karyawan di supermarket terkenal ingin membuat pembeli lebih tertib dan tidak menyerobot antrian di kasir. Ia akan menyusun nomor antre yang terdiri dari tiga angka. Apabila nomor antrian tersebut tidak memiliki angka yang sama yang dibentuk dari angka 0, 1, 2, 3, maka ada berapa banyak cara pilihan nomor antrian yang dapat dibuat karyawan tersebut?

Jawaban:

Banyak angka yang tersedia= 4 yang terdiri dari 0, 1, 2, 3

Karyawan akan memilih 3 nomor antrian berbeda, maka banyak pilihannya adalah permutasi 3 dari 4

P(n,r) = n!/(n-r)!

P(4,3) = 4!/(4-3)!

= 4!/1!

= 4 x 3 x 2 x 1 = 24 
Baca Juga: Cara Mencari FPB dan KPK Materi Matematika, Lengkap dengan Contoh Soal

Baca berita update lainnya dari Sonora.id di Google News.