Sonora.ID – Artikel ini berisi contoh soal persamaan eksponen lengkap dengan kunci jawabannya, yang diharapkan dapat membantu para siswa dalam mengusai materi ini.

Matematika merupakan jenis mata pelajaran yang membutuhka banyak latihan agar bisa menyelesaikannya.

Nah, salah satu materi matematika yang akan ditemui para siswa di kelas 10 adalah soal persamaan eksponen.

Eksponen merupakan bentuk perkalian suatu bilangan dengan dirinya sendiri sebanyak pangkatnya.

Nah, berikut contoh soal persamaan eksponen lengkap dengan kunci jawabannya yang bisa dijadikan latihan bagi para siswa.

Baca Juga: Cara Mengubah Pecahan Biasa ke Pecahan Campuran dengan Mudah

1. Tentukan penyelesaian dari persamaan ekponensial berikut ini  2^2x-7 = 8^1-x

Jawab:

Pertama-tama yang perlu kamu lakukan yaitu menyamakan basis pada kedua ruas [ruas kanan dan ruas kiri] seperti berikut:

2^2x-7 = 8^1-x
2^2x-7 = (2³)^1-x
2^2x-7 = 2^3-3x

Nahhhh karena basismya telah sama, maka dengan mudah kita dapat menentukan nilai x-nya seperti berikut ini.

2x – 7 = 3 – 3x
5x = 10
x = 2

Sehingga kita peroleh x = 2

2. Jika a dan b bilangan bulat positif yang memenuhi a^b = 2²⁰ – 2¹⁹ , maka nilai a + b = …

Jawab:

Dengan menggunakan sifat pangkat dan sifat distributif, diperoleh:

a^b = 2²⁰ – 2¹⁹

a^b = 2¹⁹ . 2 – 2¹⁹

a^b = 2¹⁹ . (2-1)

Dari sini, kita peroleh a = 2 dan b = 9 sehingga a + b = 2 + 19 = 21

3. Diketahui p dan q merupakan bilangan bulat yang bisa memenuhi persamaan . Berapakah nilai p² + q²?

Jawab:

Mula-mula, kamu harus mencari masing-masing nilai p dan q.

Dengan demikian, nilai p² + q² adalah (2)² + (-3)² = 4 + 9 = 13.

Jadi, nilai p² + q² = 13.

4. Jika , tentukan nilai b (dalam p) yang memenuhi persamaan berikut.

Jawab:

Gunakan cara seperti berikut.

Jadi, nilai b (dalam p) yang memenuhi persamaan tersebut adalah b = 1 – p.

5. Tentukan penyelesaian dari

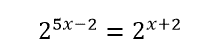
Jawab:

Basis kedua ruas sudah sama, sehingga berlaku bentuk persamaan ketiga:

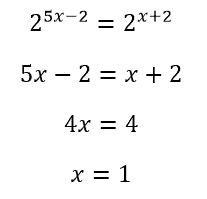
Jadi penyelesaian persamaan diatas adalah x=1.

Baca Juga: 15 Contoh Soal Himpunan Matematika, Beserta Kunci Jawabannya!

6. Tentukan nilai x yang memenuhi persamaan eksponensial berikut

3ˣ⁺²+3ˣ=10

Jawab:

3ˣ⁺²+3ˣ=10
3ˣ(3²+1)=10

3ˣ(10)=10
3ˣ = 1
3ˣ=3⁰
x=0

7. Tentukan penyelesaian dari 3^2x-2 = 5^x-1

Jawab:

Kedua basis pada persamaan diatas berbeda dan tidak ada sifat-sifat perpangkatan yang dapat kita gunakan untuk menyamakan kedua basis tersebut.

Namun, kedua pangkatnya bisa kita samakan menjadi sebagai berikut :

3^2x-2 = 5^x-1
3^2(x-1) = 5^x-1
9^x-1 = 5^x-1

Sehingga berdasarkan sifat 2, maka akan diperoleh sebagai berikut:

x – 1 = 0
     x = 1

Dengan demikian nilai x yang kita peroleh yaitu 1.

8. Tentukan penyelesaian soal berikut ini

Jawab:

Samakan basis kedua persamaan diatas,

Setelah basis sudah sama, maka berlaku penyelesaian bentuk ketiga,

3x-2=4
3x=6
x=2

Jadi, penyelesaian persamaan diatas adalah x=2.

9. Tentukan penyelesaian dari

Jawab:

Persamaan diatas memiliki basis yang berbeda, akan tetepi memiliki pangkat yang sama yaitu mengandung varibel x.

Oleh karena itu, berdasarkan bentuk ke empat yaitu, a^f(x) = b^f(x), maka f(x)=0.

x-1= 0
x= 1

Jadi, penyelesaian dari persamaan diatas adalah x=1.

9 ^x²+x = 27 ^x²-1

Jawab:

9 ^x²+x = 27 ^x²-1
3 ^2(x²+x) = 3 ^3(x²-1) 
2 (x²+x) = 3 (x²-1)
2x² + 2x = 3x² – 3
x² – 2x – 3 = 0
(x – 3) (x + 1) = 0 
x = 3     atau   x = -1    

Jadi himpunan penyelesaiannya adalah { -1,3 }

Baca berita update lainnya dari Sonora.id di Google News.

Baca Juga: Limas Segi Empat: Sifat, Rumus dan Contoh Soalnya Mudah Dimengerti