Bagikan :
| a. (13, −20) | b. (13, −4) | c. (4, 20) | d. (−5, −4) | e. (−5, −20) |
3. Titik ???? ditranslasikan oleh ???? = (6-3) menghasilkan titik ????′(4, −2). Koordinat titik ???? adalah …
| a. (10, −5) | b. (10,1) | c. (2, −1) | d. (−2,1) | e. (−2, −1) |
4. Diketahui translasi ???? memetakan titik ????(−4, 2) ke titik ????′(−1, 6). Translasi ???? akan memetakan titik ????(3, −2) ke titik …
| a. ???? ′ (0,4) | b. ???? ′ (0, 2) | c. ???? ′ (0, −6) | d. ???? ′ (6, −6) | e. ???? ′ (6, 2) |
Baca Juga: Contoh Soal Ujian Sekolah Matematika Kelas 9 dan Kunci Jawabannya
5. Segitiga PQR mempunyai koordinat ????(−3, 4),????(−1,0), dan ????(0, 2). Segitiga PQR ditranslasikan oleh ???? menghasilkan bayangan segitiga ????′????′????′. Jika koordinat titik ????′(1, −2), koordinat titik ????′ dan ????′ berturut-turut adalah …
| a. (3, −6) dan (4, −4) | b. (3, −6) dan (−4, 4) | c. (−3, 6) dan (4, −4) | d. (−3, 6) dan (−4, 4) | e. (−3, −6)dan (4, −4) |
6. Segitiga ABC ditranslasi sehingga menghasilkan bayangan ΔKLM. Diketahui koordinat A (3, 9), B (-1,4), K (4, 2), dan M (6, -3), Tentukan koordinat C dan L. Tentukan pula translasinya.
Jawab:
Untuk menentukan koordinat titik C dan L, kita terlebih dahulu menemukan translasinya. Caranya adalah:
Koordinat C = koordinat M dikurang translasi, C = ( 6 - 1, -3 - (-7)), ? C (5, 4)
Koordinat L = koordinat B ditambah translasi, L (-1 + 1, 4 + (-7)), ? L (0, -3)
Baca Juga: Matematika: 11 Contoh Soal Eksponen Kelas 10 beserta Jawabannya Mudah
7. Perhatikan gambar di bawah ini
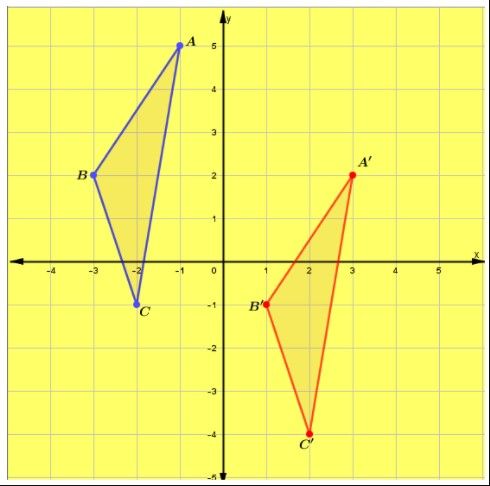
Segitiga ABC ditranslasikan 4 satuan ke kanan dan 3 satuan ke bawah, maka koordinat bayangan adalah:
A (-1,5) → A' (-1+4, 5+(-3)) atau A' (3,2)
B (-3,2) → B' (-3+4, 2+(-3)) atau B' (1,-1)
C (-2,-1) → C' (-2+4, -1+(-3)) atau C' (2,-4)
8. Koordinat titik P diketahui sebesar (4,-1). Oleh karena translasi (2a) diperoleh bayangan titik P yaitu P'(-2a, -4). Tentukanlah nilai a.
Demikian tadi contoh soal translasi beserta jawabannya lengkap dengan gambar. Semoga membantu!
