Bagikan :
:quality(50)/photo/2023/03/29/contoh-soal-translalasijpg-20230329073825.jpg)
Sonora.ID - Simak selengkapnya pembahasan mengenai contoh soal translasi beserta jawabannya lengkap dengan gambar yang ada dalam pelajaran matematika berikut ini.
Matematika memiliki berbagai cabang ilmu, salah satunya adalah cabang ilmu geometri yang disebut pula Transformasi Geometri.
Dilansir dari Gramedia, apabila diibaratkan, transformasi adalah proses perpindahan suatu benda dari suatu kedudukan ke kedudukan lain.
Keberadaan transformasi geometri pun mempunyai banyak cakupan, yang pertama yakni translasi atau pergeseran.
Prinsip dasar dari translasi adalah suatu bentuk transformasi yang melibatkan pergerakan setiap titik pada bidang tertentu dengan memperhitungkan arah dan jarak yang spesifik.
Baca Juga: Rumus Keliling Persegi dan Contoh Soalnya dalam Matematika
Contoh Soal Translasi
Adapun sejumlah contoh soal latihan translasi dapat kamu perhatikan di bawah ini dirangkum dari Gramedia dan Kompas.com.
1. Tentukan hasil bayangan titik ????(3, 5) oleh translasi ???? (-24)!
| a. A’ (5, 1) | b. A’ (3, 7) | c. A’ (7, -1) | d. A’(7, 3) | e. A’ (1, 9) |
2. Diketahui titik ????′(4, −12) adalah bayangan titik P oleh translasi ???? = (-98). Koordinat titik ???? adalah …
| a. (13, −20) | b. (13, −4) | c. (4, 20) | d. (−5, −4) | e. (−5, −20) |
3. Titik ???? ditranslasikan oleh ???? = (6-3) menghasilkan titik ????′(4, −2). Koordinat titik ???? adalah …
| a. (10, −5) | b. (10,1) | c. (2, −1) | d. (−2,1) | e. (−2, −1) |
4. Diketahui translasi ???? memetakan titik ????(−4, 2) ke titik ????′(−1, 6). Translasi ???? akan memetakan titik ????(3, −2) ke titik …
| a. ???? ′ (0,4) | b. ???? ′ (0, 2) | c. ???? ′ (0, −6) | d. ???? ′ (6, −6) | e. ???? ′ (6, 2) |
Baca Juga: Contoh Soal Ujian Sekolah Matematika Kelas 9 dan Kunci Jawabannya
5. Segitiga PQR mempunyai koordinat ????(−3, 4),????(−1,0), dan ????(0, 2). Segitiga PQR ditranslasikan oleh ???? menghasilkan bayangan segitiga ????′????′????′. Jika koordinat titik ????′(1, −2), koordinat titik ????′ dan ????′ berturut-turut adalah …
| a. (3, −6) dan (4, −4) | b. (3, −6) dan (−4, 4) | c. (−3, 6) dan (4, −4) | d. (−3, 6) dan (−4, 4) | e. (−3, −6)dan (4, −4) |
6. Segitiga ABC ditranslasi sehingga menghasilkan bayangan ΔKLM. Diketahui koordinat A (3, 9), B (-1,4), K (4, 2), dan M (6, -3), Tentukan koordinat C dan L. Tentukan pula translasinya.
Jawab:
Untuk menentukan koordinat titik C dan L, kita terlebih dahulu menemukan translasinya. Caranya adalah:
Koordinat C = koordinat M dikurang translasi, C = ( 6 - 1, -3 - (-7)), ? C (5, 4)
Koordinat L = koordinat B ditambah translasi, L (-1 + 1, 4 + (-7)), ? L (0, -3)
Baca Juga: Matematika: 11 Contoh Soal Eksponen Kelas 10 beserta Jawabannya Mudah
7. Perhatikan gambar di bawah ini
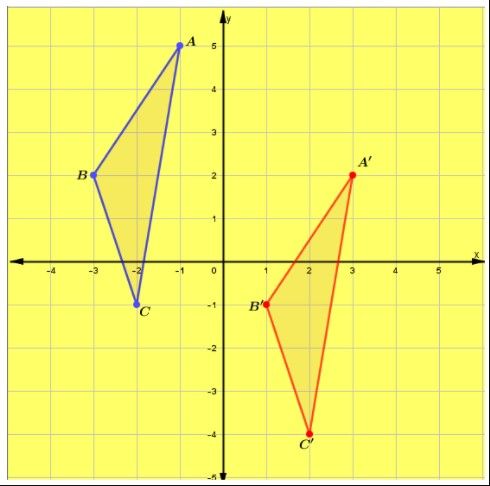
Segitiga ABC ditranslasikan 4 satuan ke kanan dan 3 satuan ke bawah, maka koordinat bayangan adalah:
A (-1,5) → A' (-1+4, 5+(-3)) atau A' (3,2)
B (-3,2) → B' (-3+4, 2+(-3)) atau B' (1,-1)
C (-2,-1) → C' (-2+4, -1+(-3)) atau C' (2,-4)
8. Koordinat titik P diketahui sebesar (4,-1). Oleh karena translasi (2a) diperoleh bayangan titik P yaitu P'(-2a, -4). Tentukanlah nilai a.
Demikian tadi contoh soal translasi beserta jawabannya lengkap dengan gambar. Semoga membantu!
:quality(50)/photo/2024/12/23/balasan-ucapan-selamat-nataljpg-20241223033947.jpg)
:quality(50)/photo/2024/12/23/featured-neww-2024-12-23t15360-20241223033625.jpg)
:quality(50)/photo/2024/12/20/img_1583jpg-20241220053709.jpg)
:quality(50)/photo/2024/12/23/merrychristmasjpg-20241223113138.jpg)